1) The document discusses complexity analysis of algorithms, which involves determining the time efficiency of algorithms by counting the number of basic operations performed based on input size.
2) It covers motivations for complexity analysis, machine independence, and analyzing best, average, and worst case complexities.
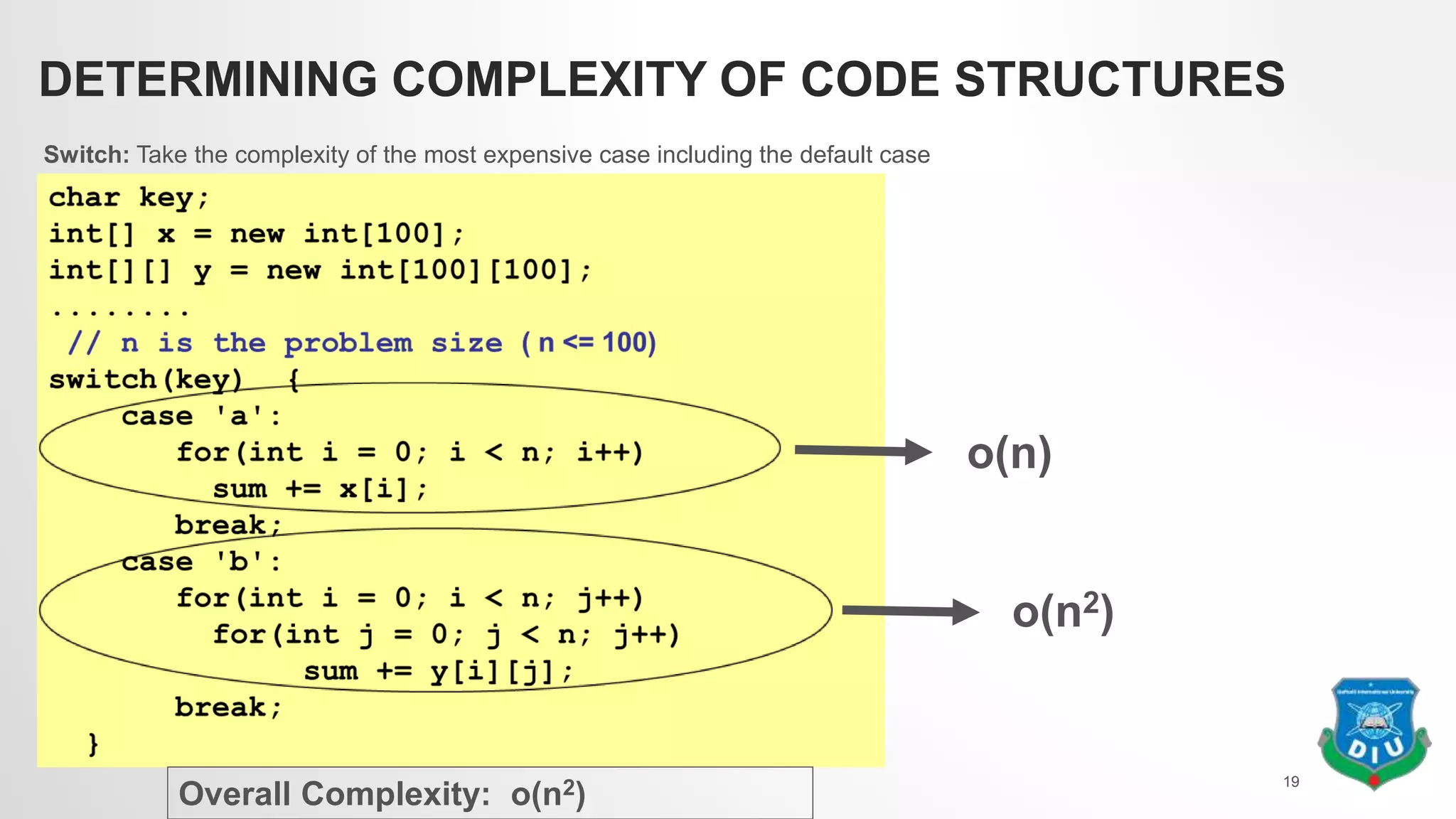
3) Simple rules are provided for determining the complexity of code structures like loops, nested loops, if/else statements, and switch cases based on the number of iterations and branching.









![SIMPLE COMPLEXITY ANALYSIS: LOOP
EXAMPLE
• Find the exact number of basic operations in the following program fragment:
• There are 2 assignments outside the loop => 2 operations.
• The for loop actually comprises
• an assignment (i = 0) => 1 operation
• a test (i < n) => n + 1 operations
• an increment (i++) => 2 n operations
• the loop body that has three assignments, two multiplications, and an addition => 6 n operations
Thus the total number of basic operations is 6 * n + 2 * n + (n + 1) + 3
= 9n + 4
11
double x, y;
x = 2.5 ; y = 3.0;
for(int i = 0; i < n; i++){
a[i] = x * y;
x = 2.5 * x;
y = y + a[i];
}](https://image.slidesharecdn.com/complexityanalysis-180102031642/75/Complexity-analysis-in-Algorithms-11-2048.jpg)






![DETERMINING COMPLEXITY OF CODE
STRUCTURES
O(if-else) = Max[O(Condition), O(if), O(else)]
18](https://image.slidesharecdn.com/complexityanalysis-180102031642/75/Complexity-analysis-in-Algorithms-18-2048.jpg)