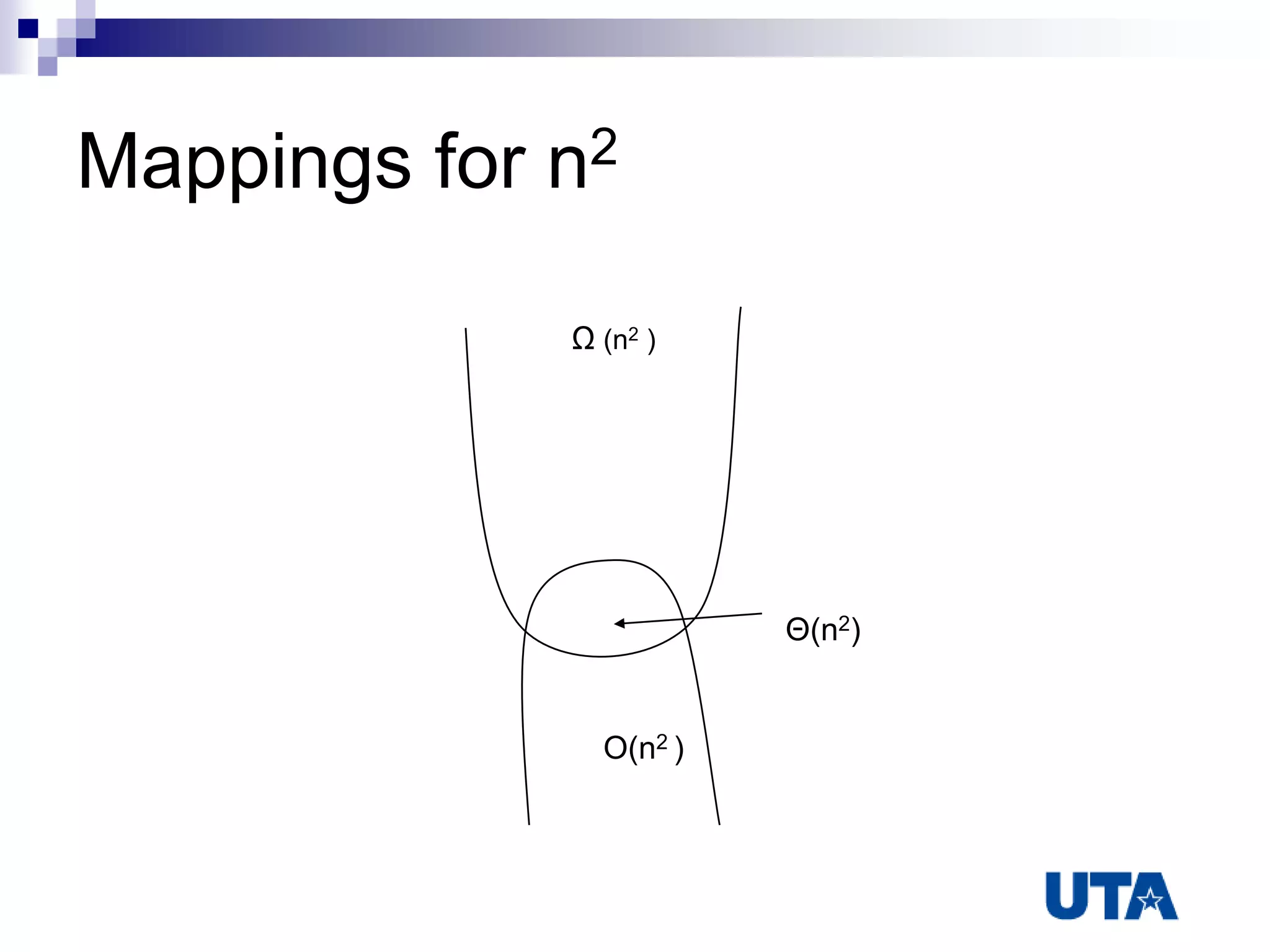
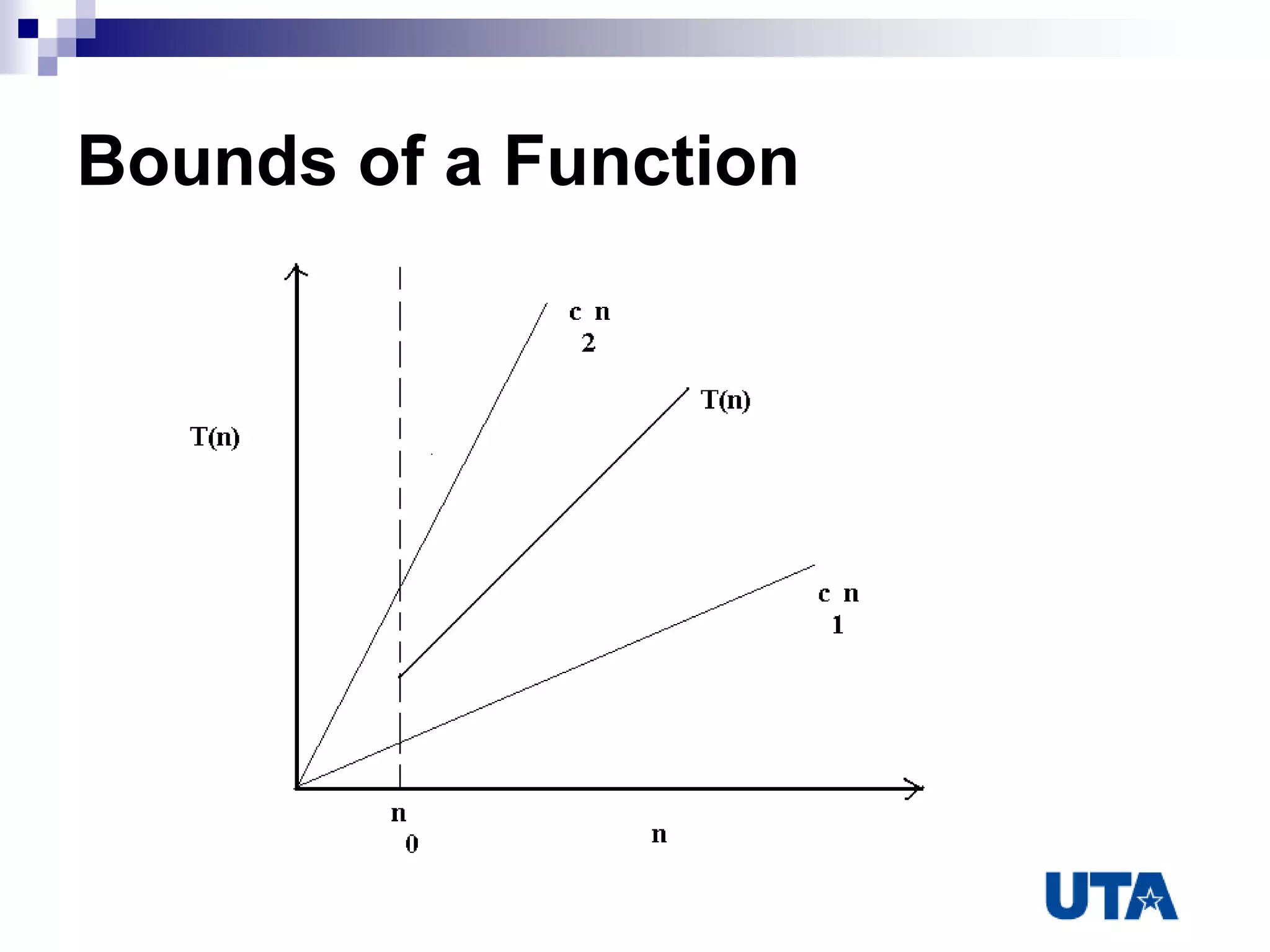
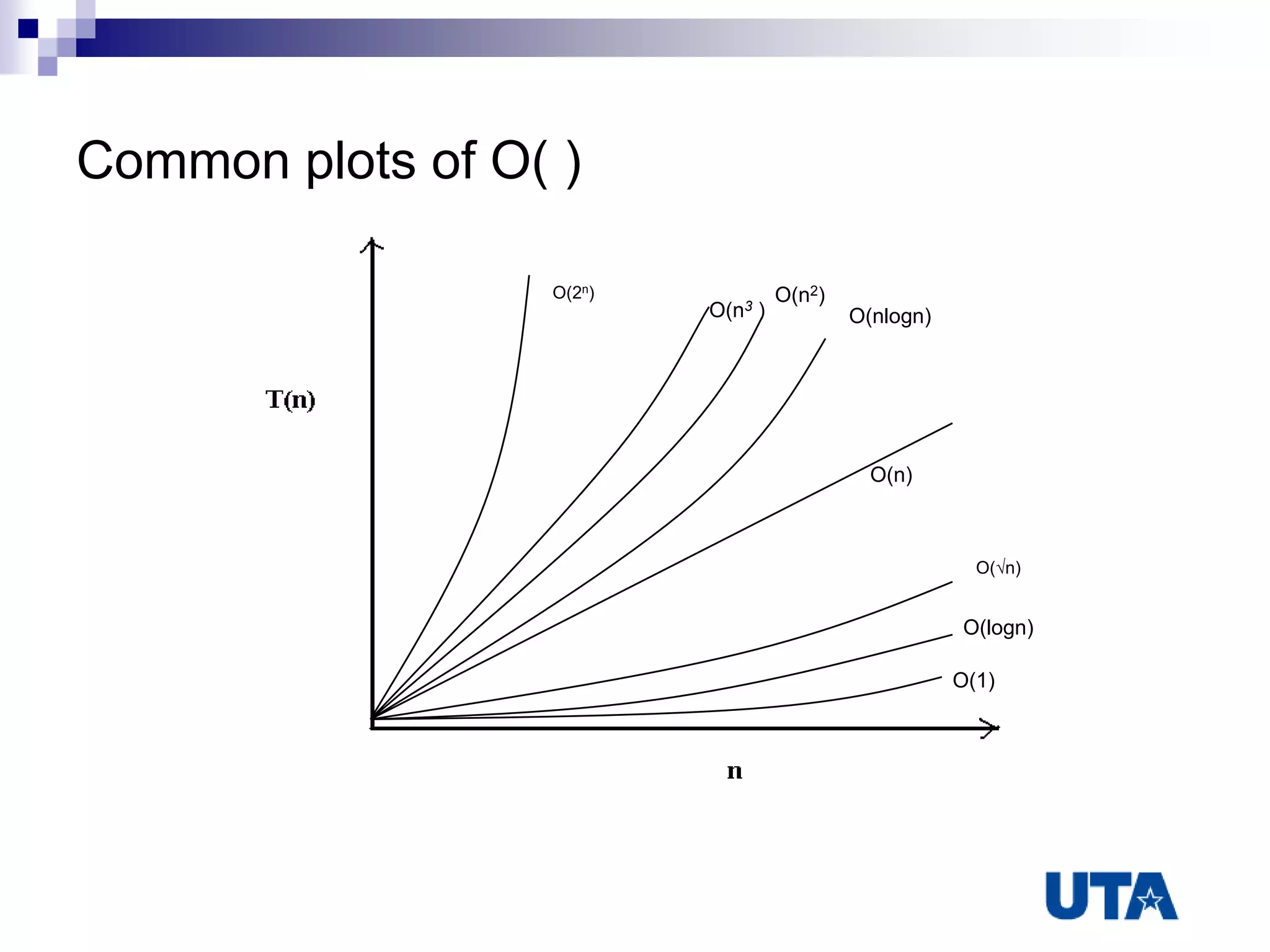
This document discusses algorithms and their analysis. It defines an algorithm as a step-by-step procedure to solve a problem or calculate a quantity. Algorithm analysis involves evaluating memory usage and time complexity. Asymptotics, such as Big-O notation, are used to formalize the growth rates of algorithms. Common sorting algorithms like insertion sort and quicksort are analyzed using recurrence relations to determine their time complexities as O(n^2) and O(nlogn), respectively.



![Sample Algorithm
FINDING LARGEST NUMBER
INPUT: unsorted array „A[n]‟of n numbers
OUTPUT: largest number
----------------------------------------------------------
1 large ← A[j]
2 for j ← 2 to length[A]
3 if large < A[j]
4 large ← A[j]
5 end](https://image.slidesharecdn.com/week1-140403005730-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHMS-4-2048.jpg)