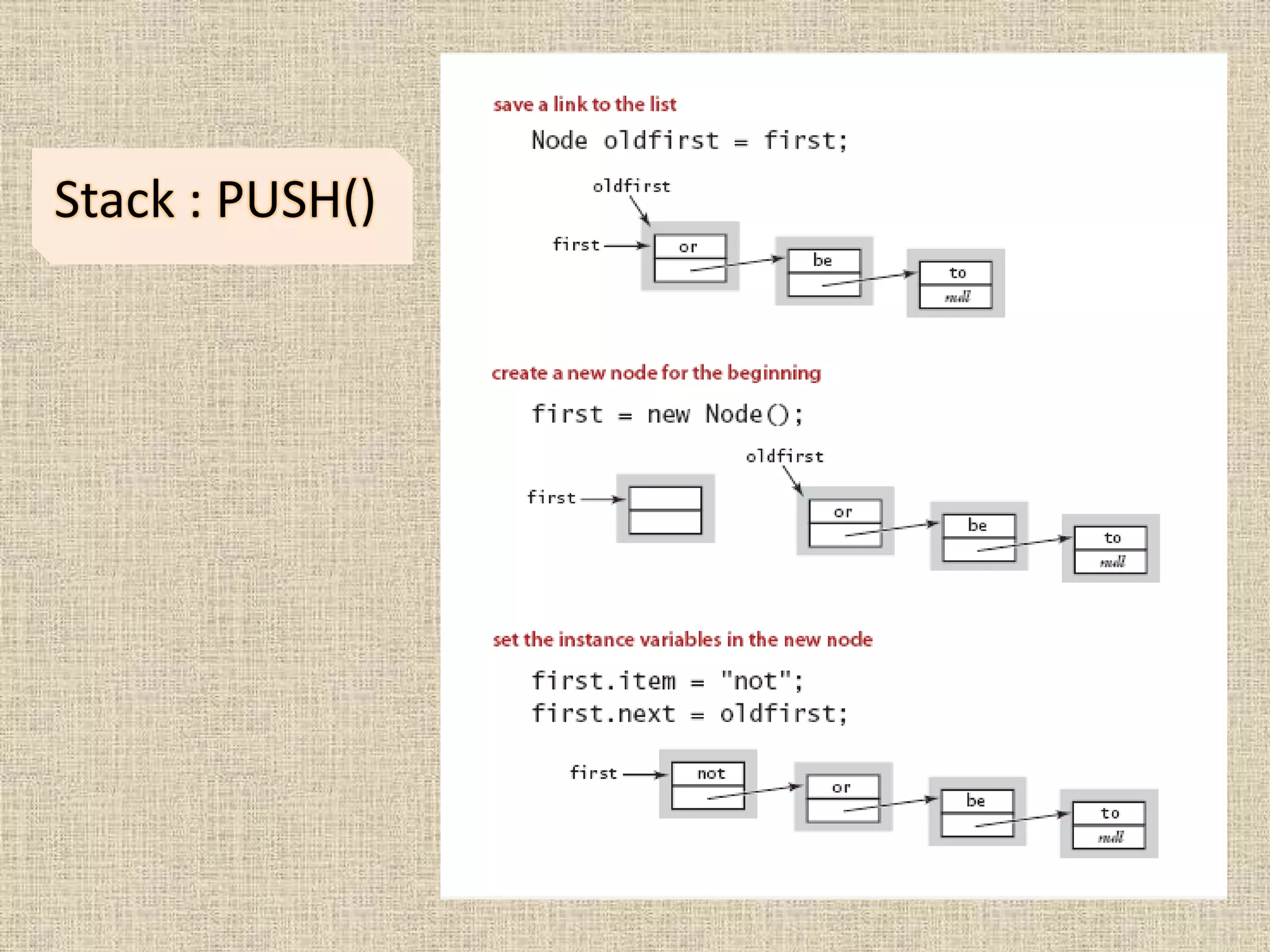
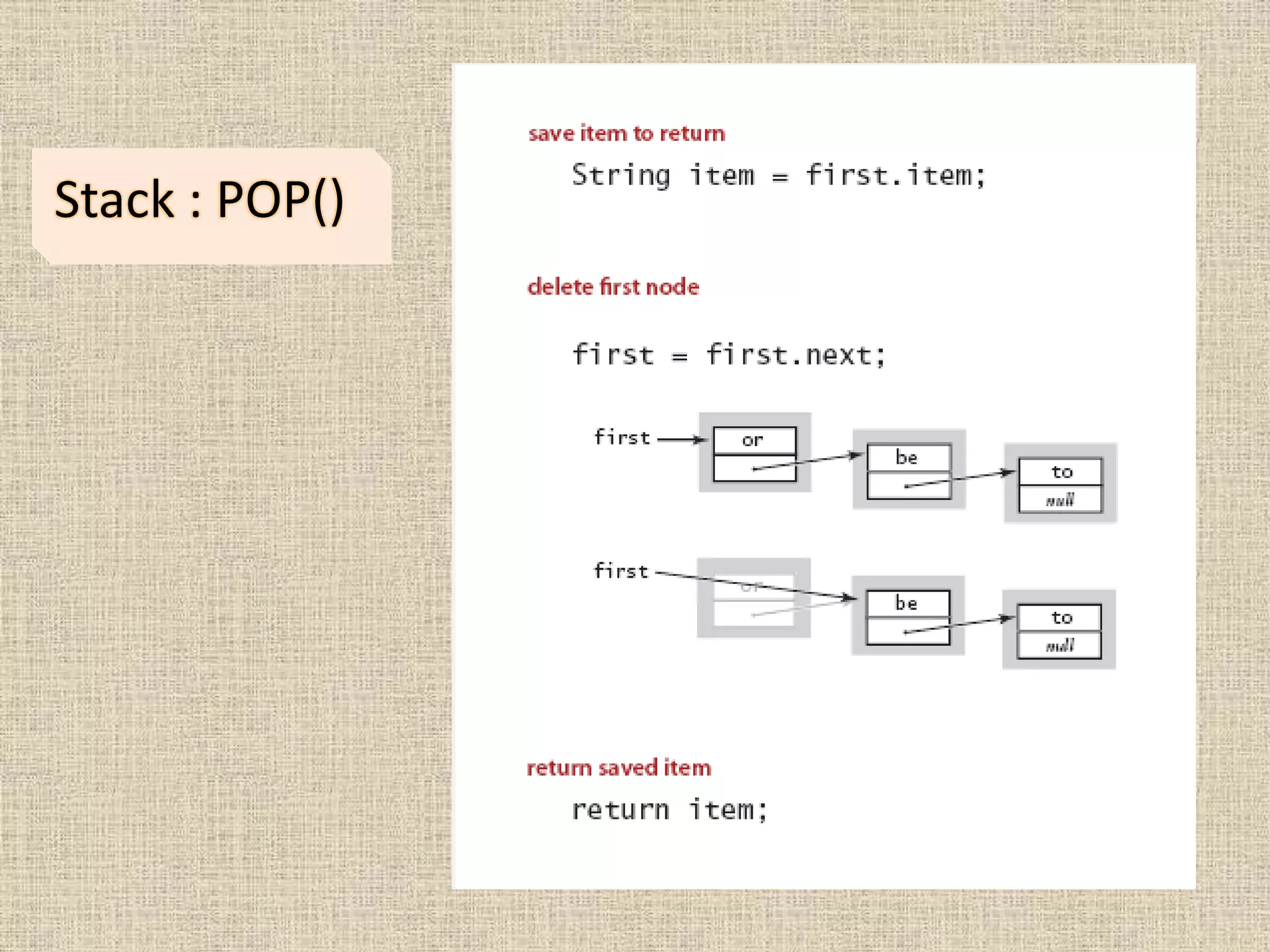
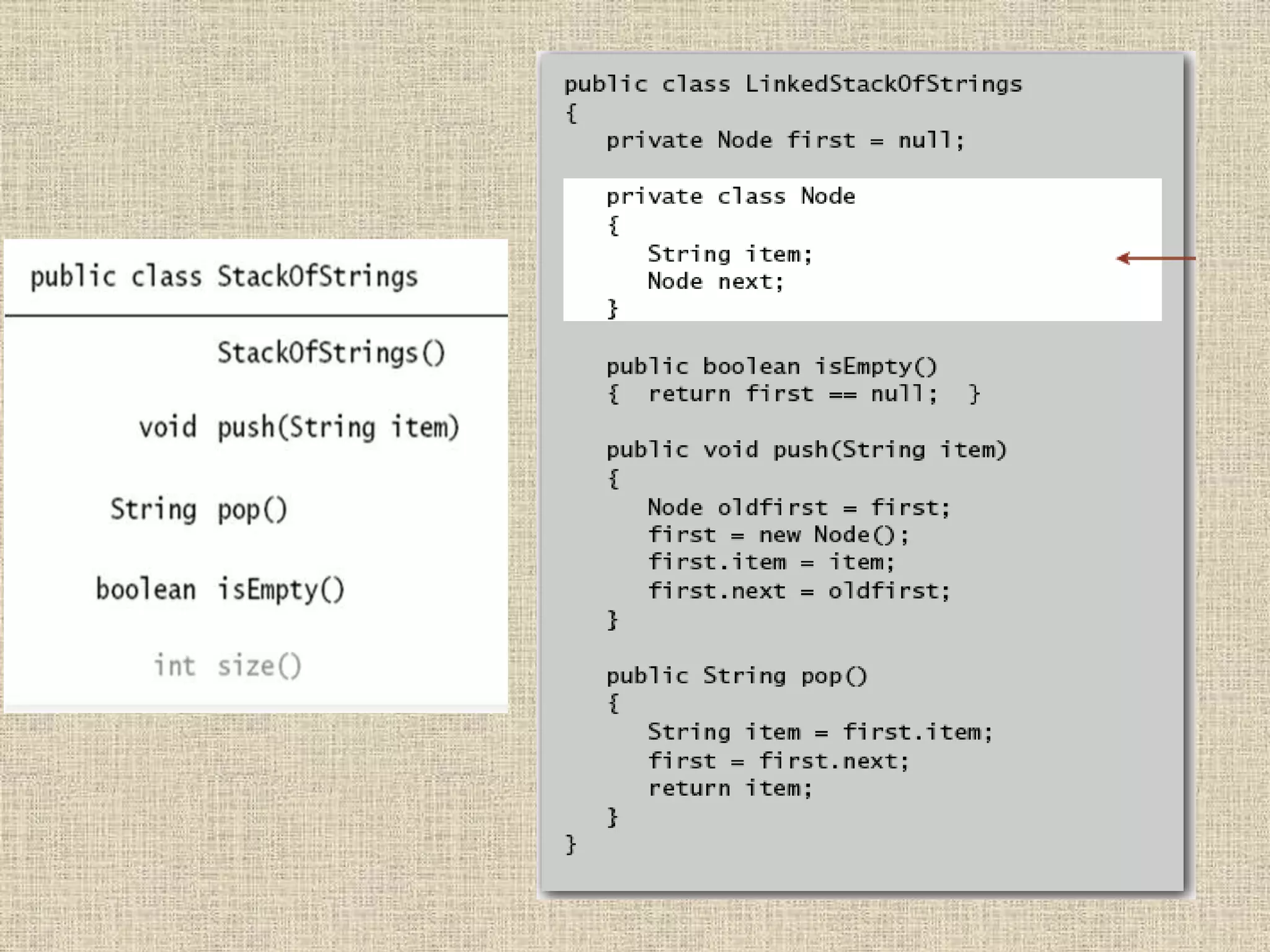
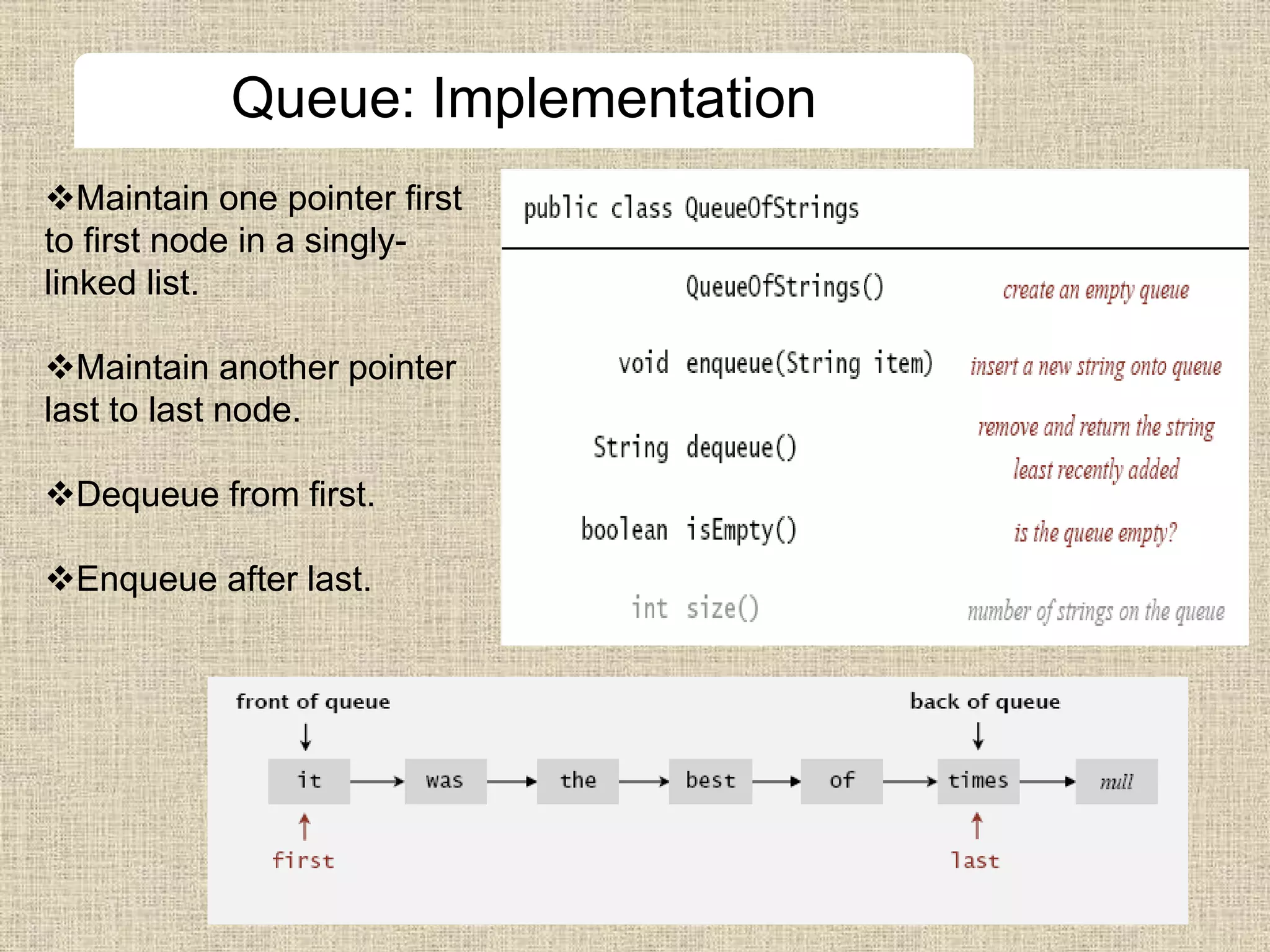
The document discusses stacks and queues, which are fundamental data structures that can insert and remove items. Stacks follow the LIFO (last in, first out) principle, while queues follow the FIFO (first in, first out) principle. The document provides implementations of stacks and queues using linked lists and arrays and examples of their applications in parsing, compilers, undo functions, and more.






![Fixed-capacity stack: array implementation
Use array s[] to store N items on stack.
push(): add new item at s[N].
pop(): remove item from s[N-1].
Defect. Stack overflows when N exceeds capacity.](https://image.slidesharecdn.com/stackandqueue-140701050837-phpapp02/75/Stack-and-queue-10-2048.jpg)






![Token Operator Precedence Association
( )
[ ]
-> .
function call
array element
struct or union member
17 left-to-right
-- ++ increment, decrement2
16 left-to-right
-- ++
!
-
- +
& *
sizeof
decrement, increment3
logical not
one’s complement
unary minus or plus
address or indirection
size (in bytes)
15 right-to-left
(type) type cast 14 right-to-left
* / % mutiplicative 13 Left-to-right
Operator Precedence](https://image.slidesharecdn.com/stackandqueue-140701050837-phpapp02/75/Stack-and-queue-19-2048.jpg)